Absorbing spheres

As noted on the previous page, non-absorbing materials have real values of refractive index m = n + i k. Absorbing materials have complex values of refractive index.: for example, in the visible spectrum, the refractive index of water has a very small imaginary component, such as 1.33257 + i 0.0000000164 at a wavelength λ = 0.65 µm. In practice, it is usual to ignore the imaginary component in calculations of scattering from water - thus assuming that water is non-absorbing.

Fig. 1 Scattering of red light (wavelength λ = 0.65 µm) from a sphere of radius 100 µm for refractive indices of 1.33257 and 1.33257 + i 1000

Fig. 1 shows the effect of absorption on scattering of red light from a sphere with r = 100 µm: the red/brown curves show results for a refractive index of 1.33257 (i.e. non-absorbing), whilst the blue curves show results for a refractive index of 1.33257 + i1000 (i.e. very absorbing). For the non-absorbing sphere, the primary rainbow and its supernumerary arcs are clearly visible at scattering angles around 140°. For the absorbing sphere, the scattered intensity is constant between 30° and 180° - and, perhaps surprisingly, almost as strong as the primary rainbow for the non-absorbing sphere. For the absorbing sphere, the scattered light is the vector sum of light diffracted by the sphere and light reflected from the exterior of the sphere. Diffraction is the dominant mechanism between 0° and 30° but Fig. 2 below shows that the intensity of the light reflected from the exterior of an absorbing sphere is independent of scattering angle - coinciding with the constant intensity shown in Fig. 1 between 30° and 180°.

Fig. 2 As Fig. 1, but showing only external reflection from a sphere of radius 100 µm for refractive indices of 1.33257 and 1.33257 + i 1000

Calculations using the Debye series can be useful to explain various scattering phenomena - as shown elsewhere on this site. Although the method originally used in MiePlot v2.0 to calculate spherical Bessel functions of first kind j_n(z) and second kind y_n(z) was reliable for real values of z, it was unreliable for complex values of z. Consequently, MiePlot's implementation of the Debye series algorithm had to be limited to real values of refractive index. An elegant solution to this problem was given by William Lentz in his paper "Generating Bessel functions in Mie scattering calculations using continued fractions" (Applied Optics, 15, 668 - 671, 1976). As a result of invaluable personal guidance and source code provided by William Lentz, MiePlot (available here) now uses his method of "continued fractions" - thus allowing MiePlot's implementation of the Debye series to cover complex values of refractive index. An example of MiePlot's output is shown below in Fig. 2.

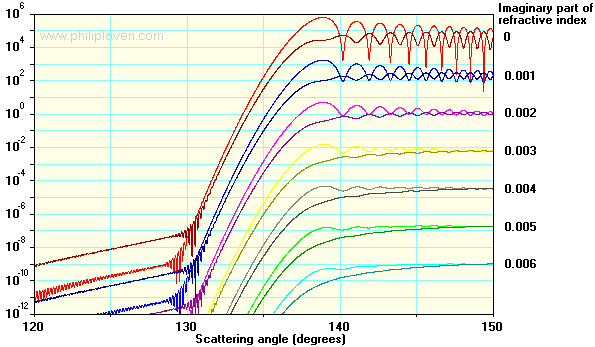
Fig. 3 Debye series (p = 2) scattering of red light (wavelength λ = 0.65 µm) from a sphere with radius r = 100 µm for real refractive index of 1.33257 and different values of imaginary refractive index.

Fig. 3 demonstrates that the p = 2 rays (those suffering one internal reflection and generating the primary rainbow) reduce in intensity as the imaginary value of refractive index is increased, in line with the following formula:

I = I₀ exp(– 4 π k L / λ)
where I₀ is the incident intensity
λ is the wavelength
I is the intensity after traversing distance L within a medium with imaginary value of refractive index k

Fig. 4 Debye series p = 0 and p = 2 scattering of red light (wavelength λ = 0.65 µm) from an absorbing sphere with radius r = 100 µm (refractive index = 1.33257 + i 0.001)

Fig. 4 shows that, for refractive index = 1.33257 + i 0.001 (mildly absorbing), the intensity of the Debye p = 0 contribution (due to diffraction and external reflection) is greater than that of the p = 2 rays.

Fig 5 Mie scattering of red light (wavelength λ = 0.65 µm) from an absorbing sphere with radius r = 100 µm (refractive index = 1.33257 + i 0.001)

Fig. 6 Comparison of Mie scattering with the vector sum of Debye p = 0 and p = 2 contributions for scattering of red light (wavelength λ = 0.65 µm) from an absorbing sphere with radius r = 100 µm (refractive index = 1.33257 + i 0.001)

Fig. 7 Comparison of Mie scattering with the vector sum of Debye p = 0, p = 2 and p = 3 contributions for scattering of red light (wavelength λ = 0.65 µm) from an absorbing sphere with radius r = 100 µm (refractive index = 1.33257 + i 0.001)

Figs. 5, 6 and 7 compare Mie theory and Debye series calculations for scattering angles between 120° and 150° (for the same conditions as Fig. 4). In all of graphs, the results of Mie theory calculations are shown by red (and brown) curves. In Fig. 6, the blue curves showing the vector sum of the Debye series p = 0 and p = 2 calculations have been superimposed on the red curves showing the Mie theory results. The rapid oscillations in intensity above 132° are due to interference between the p = 0 and p = 2 rays. Note that the red curves are barely visible in Fig. 6, except for scattering angles below 132°, where the Debye p = 3 rays must be taken into account. The blue curves in Fig. 7 show the vector sum of the Debye p = 0, p = 2 and p = 3 rays. As the red curves are not visible in Fig.7, it is obvious that the p = 0, p = 2 and p = 3 contributions are the dominant scattering mechanisms for this range of scattering angles – and, more importantly, that the two independent methods of calculation give essentially identical results.

Page updated on 30 November 2003

Previous page: Refractive index of water

Contents

Next page:MiePlot program